HW4

문제 1

정규분포 pdf 값을 계산하는 자신만의 파이썬 함수를 정의하고 정규분포 mu = 3, sigma = 2 의 pdf를 그릴 것.

import pandas as pd
import numpy as np    
from scipy.stats import norm
import matplotlib.pyplot as plt    
import seaborn as sns    

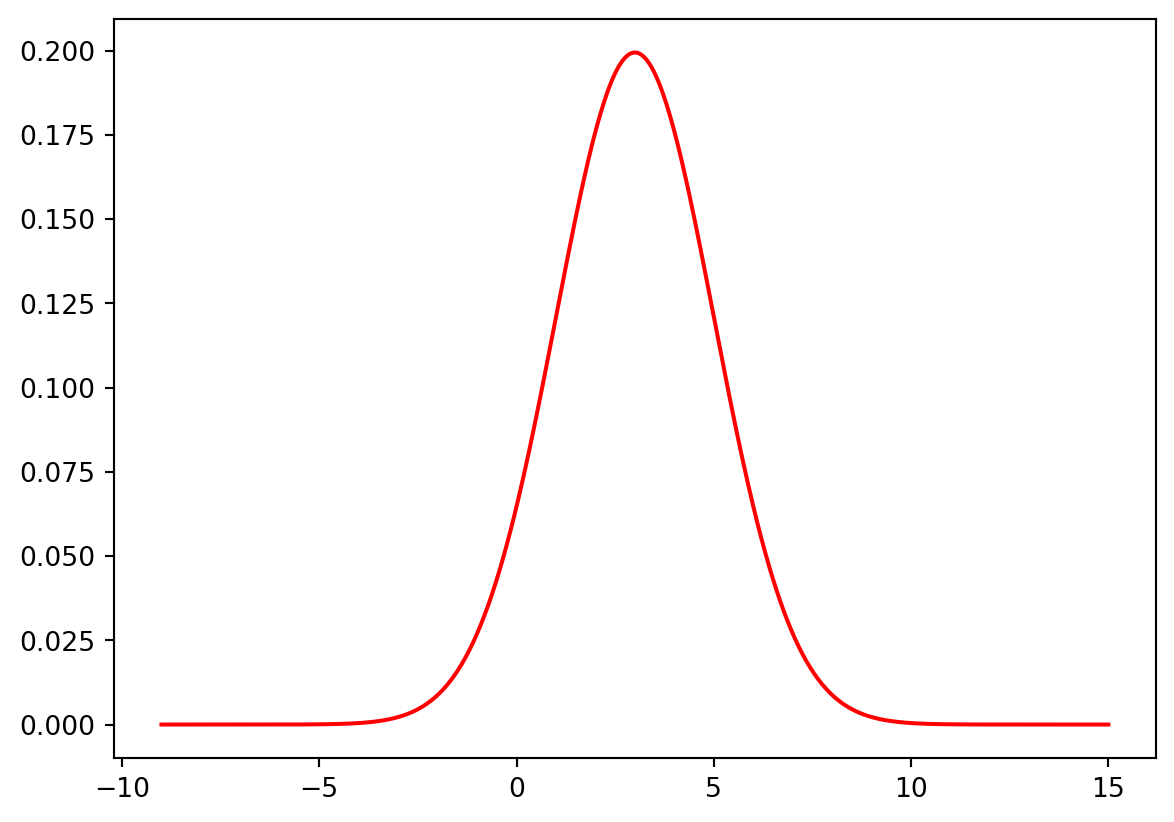
def my_norm(x,mu,sigma):
    #x=np.linspace(-10,10,500)
    y=norm.pdf(x, loc=mu, scale= sigma)
    plt.plot(x,y,color="red")
    plt.show()
my_norm(np.linspace(-9,15,500),3,2)

---

문제 2

파이썬 scipy 패키지 사용해서 다음과 같은 확률을 구하시오.

X ~ N(2, 3^2)

• 1. P(X < 3)

from scipy import *
a=norm.cdf(3,loc=2,scale=3)
print(f"정규분포 N(2, 3^2)를 따르는 X의 P(X < 3) 는 {a}")

정규분포 N(2, 3^2)를 따르는 X의 P(X < 3) 는 0.6305586598182363

• 2. P(2 < X < 5)

b=norm.cdf(5,loc=2,scale=3)-norm.cdf(2,loc=2,scale=3)
print(f"정규분포 N(2, 3^2)를 따르는 X의 P(2 < X < 5) 는 {b}")

정규분포 N(2, 3^2)를 따르는 X의 P(2 < X < 5) 는 0.3413447460685429

• 3. P(X < 3 or X > 7)

c=1-norm.cdf(7,loc=2,scale=3)+norm.cdf(3,loc=2,scale=3)
print(f"정규분포 N(2, 3^2)를 따르는 X의 P(X < 3 or X > 7) 는 {c}")

정규분포 N(2, 3^2)를 따르는 X의 P(X < 3 or X > 7) 는 0.678349012091051

---

문제 3

LS 빅데이터 스쿨 학생들의 중간고사 점수는 평균:30, 분산:4인 정규분포를 따른다. 상위 5%에 해당하는 학생의 점수는?

# 상위 0.05= 하위 0.95 이므로
exam=norm.ppf(0.95,30,2)
print(f"상위5%에 해당하는 학생의 점수는 {exam} 점 이다.")

상위5%에 해당하는 학생의 점수는 33.28970725390295 점 이다.

exam=norm.ppf(0.95,30,2)
x=norm.pdf(np.linspace(20,40,200),loc=30,scale=2)
plt.axvline(x=exam, color="blue",linestyle="--",linewidth=3)
plt.plot(np.linspace(20,40,200),x)
plt.show()